
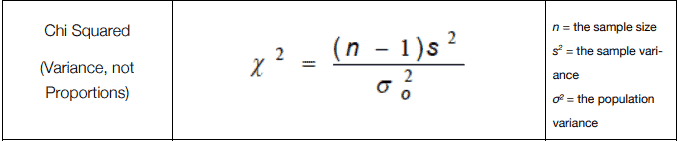
If you have a 2x2 contingency table, use this calculator. See more details in our analysis checklist.Ĭhi-square tests are also used to analyze contingency tables. Large number of subjects in each category (usually greater than 5) While chi-square is one of the more flexible tests in statistics, it has the following assumptions: While this can be done by hand, there are several opportunities for human error, which is why we recommend this calculator (or Prism for more advanced analysis). Once you have calculated the test statistic, you would need to use a computer or a chi-square table to find the approximate P value.
By summing up the calculated values for each of the categories, we can calculate the chi-square test statistic as shown below: You can use the formula below, entering the observed (O) and expected (E) frequencies for each group. This contingency table calculator includes an option to do a Yates' correction.Ĭhi-square is not as complicated as some statistical tests and is sometimes done by hand. With contingency tables, the expected counts are determined using the assumption that the factors are not-related. This calculator allows for more flexible options beyond just that, and decimals are acceptable so long as the expected frequencies add up to the total number of observations.Ī specific use-case of chi-square is analyzing contingency tables. One common assumption is that all groups are equal (e.g.
EASY CHI SQUARE CALCULATOR HOW TO
Here is an example of how to calculate expected frequencies. We can compare the counts that we observe to the expected distribution to see if there is evidence that our sample as a whole is different from the hypothesized distribution.Ĭhi-square calculators require you to enter the expected frequencies in each group so that it knows what it is comparing against. Suppose you have 605 subjects in total spread across five categories and observe the counts for each below: Decimals in the expected count are acceptable so long as they do not represent percentages (for 15% of 250 total individuals, enter 37.5). Important: Expected frequencies (like observed) should be entered as counts. Labels for each category are not used in calculation but are often helpful to organize the input data. How to use the chi-square table calculatorĮnter the label (optional), actual counts of observed subjects (or events), and expected counts for each category on a separate line. If you are analyzing rates or percentages, then chi-square is not the appropriate tool. The key is that its focus is on count data. The expected counts can be that they are equal, are based on previous research, follow some statistical distribution, or something else entirely. It is a flexible method where the researcher must determine the expected counts for each group. "Subjects" in the experiment can be individuals, events, items, or anything else so long as it can be counted.

In other words Men and Women probably do not have a different preference for Soccer or Cricket.A chi-square test compares count data in different groups to their expected counts within each group. In this case p is greater than 0.05, so we believe the variables are independent (ie not linked together). Now, p < 0.05 is the usual test for dependence. If Gender (Man or Woman) does affect Preferred sports we say they are dependent.īy using our chi-square calculator, we come up with a "p" value: The Chi-Square Test gives a "p" value to help you decide E is the expected value Chi-square Real Time Examples


 0 kommentar(er)
0 kommentar(er)
